Расположение корней квадратного трехчлена. Квадратный трёхчлен и его корни
Описание видеоурока
Каждое из выражений три икс пятой степени минус икс четвертой степени плюс три икс куб минус шесть икс плюс два; пять игрек четвертой степени минус игрек куб плюс пять игрек квадрат минус три игрек плюс восемнадцать; три зет шестой степени минус зет четвертой степени плюс зет квадрат минус зет плюс два является многочленом с одной переменной.
Значение переменной, при котором многочлен обращается в нуль, называют корнем многочлена.
Найдем, например, корни многочлена икс куб минус четыре икс. Для этого решим уравнение икс куб минус четыре икс равно нулю. Разложив левую часть уравнения на множители, получим произведение из трех множителей: икс, икс минус два и икс плюс два, равное нулю. Отсюда икс первое равно нулю, икс второе равно два, икс третье равно минус два.
Таким образом, числа нуль, два и минус два - являются корнями многочлена икс куб минус четыре икс…
Многочлен второй степени с одной переменной называют квадратным трехчленом.
Квадратным трехчленом называется многочлен вида а икс квадрат плюс бэ икс плюс цэ, где икс -переменная, ..а, бэ и цэ -некоторые числа, причем а не равно нулю.
Коэффициент а называют старшим коэффициентом, цэ - свободным членом квадратного трехчлена.
Примерами квадратных трехчленов являются многочлены два икс квадрат минус икс минус пять; икс квадрат плюс семь икс минус восемь. В первом из них а равно два, бэ равно минус один, цэ равно минус пять, во втором а равно один, бэ равно семь, цэ равно минус восемь. К квадратным трехчленам относятся также и такие многочлены второй степени, у которых один из коэффициентов бэ либо цэ или даже оба равны нулю. Так, многочлен пять икс квадрат минус два икс считают квадратным трехчленом. Коэффициент а равен пяти, бэ равно минус двум, цэ равно нулю.
Для того чтобы найти корни квадратного трехчлена а икс квадрат плюс бэ икс плюс цэ, нужно решить квадратное уравнение а икс квадрат плюс бэ икс плюс цэ равно нулю.
Пример первый. Найдем корни квадратного трехчлена икс квадрат минус три икс минус четыре.
Для этого приравняем данное выражение к нулю и решим полученное квадратное уравнение. Дискриминант в нем равен двадцати пяти, первый корень равен четырем, второй корень равен минус одному.
Таким образом, квадратный трехчлен икс квадрат минус три икс минус четыре имеет два корня: четыре и минус один.
Так как квадратный трехчлен а икс квадрат плюс бэ икс плюс цэ имеет те же корни, что и уравнение а икс квадрат плюс бэ икс плюс цэ равно нулю, то он может, как и квадратное уравнение иметь два корня, один корень или не иметь корней вообще. Это зависит от значения дискриминанта квадратного уравнения, который также называют дискриминантом квадратного трехчлена.. Если дискриминант больше нуля, то квадратный трехчлен имеет два корня; если дискриминант равен нулю, то квадратный трехчлен имеет один корень; если дискриминант меньше нуля, то квадратный трехчлен не имеет корней.
При решении задач иногда бывает удобно представить квадратный трехчлен а икс квадрат плюс бэ икс плюс цэ в виде суммы а умноженного на квадрат разности а и эм…и числа эн, где эм и эн - некоторые числа. Такое преобразование называется выделением квадрата двучлена из квадратного трехчлена. Покажем на примере, как выполняется такое преобразование.
Второй пример. Выделить из трехчлена два икс квадрат минус четыре икс плюс шесть… квадрат двучлена.
Вынесем за скобки множитель два,.. затем преобразуем выражение в скобках, для чего прибавим и отнимем единицу… В итоге получим сумму удвоенного квадрата разности чисел икс и один… И числа четыре.
Таким образом, два икс квадрат минус четыре икс плюс шесть равно сумме удвоенного квадрата разности чисел икс и один.. И числа четыре…
Рассмотрим задачу, при решении которой используется выделение квадрата двучлена из квадратного трехчлена.
Задача. Докажем, что из всех прямоугольников с периметром 20 см наибольшую площадь имеет квадрат.
Пусть одна сторона прямоугольника равна икс сантиметров. Тогда длина второй будет десять минус икс сантиметров, а площадь прямоугольника равна произведению этих сторон.
Раскрыв скобки в выражении икс умноженное на разность десять и икс, получим десять икс минус икс квадрат. Выражение минус икс квадрат плюс десять икс представляет собой квадратный трехчлен, в котором коэффициент А равен минус один, бэ равно десяти, цэ равно нулю. Выделим квадрат двучлена и получим выражение минус квадрат разности икс и пять.. плюс двадцать пять.
Так как выражение минус квадрат разности икс и пять при любом икс не равном пяти отрицательно, то и всё выражение минус квадрат разности икс и пять… плюс двадцать пять принимает наибольшее значение при икс равном пяти.
Значит, площадь будет наибольшей, когда одна из сторон прямоугольника равна 5 см. В этом случае другая сторона также равна 5 см. Это означает, что данный прямоугольник является квадратом.
Практика экзаменов по математике показывает, что задачи с параметрами представляют наибольшую сложность как в логическом, так и в техническом плане и поэтому умение их решать во многом предопределяет успешную сдачу экзамена любого уровня.
В задачах с параметрами наряду с неизвестными величинами фигурируют величины, численные значения которых хотя и не указаны конкретно, но считаются известными и заданными на некотором числовом множестве. При этом параметры, входящие в условие, существенно влияют на логический и технический ход решения и форму ответа. Такие задачи можно найти в книге «514 задач с параметрами» В литературе по элементарной математике немало учебных пособий, задачников, методических руководств, где приводятся задачи с параметрами. Но большинство из них охватывает узкий круг вопросов, делая основной упор на рецептуру, а не на логику решения задач. К тому же наиболее удачные из книг давно стали библиографической редкостью. В конце работы дан список книг, статьи из которых помогли составить классификацию утверждений по теме работы. Наиболее значимой является пособие Шахмейстера А. Х. Уравнения и неравенства с параметрами.
Основная цель настоящей работы – восполнение некоторых содержательных пробелов основного курса алгебры и установление фактов использования свойств квадратичной функции, позволяющие существенно упростить решение задач, связанных с расположением корней квадратного уравнения относительно некоторых характерных точек.
Задачи работы:
Установить возможные случаи расположения корней квадратного трехчлена на числовой прямой;
Выявить алгоритмы, позволяющие решать квадратные уравнения с параметром на основе использования расположения корней квадратного трехчлена на числовой прямой;
Научиться решать задачи более высокой, по сравнению с обязательным уровнем, сложности; овладеть рядом технических и интеллектуальных математических умений на уровне свободного их использования; повысить математическую культуру в рамках школьного курса математики.
Объект исследования: расположение корней квадратного трехчлена на координатной прямой.
Предмет исследования: квадратные уравнения с параметром.
Способы исследования. Основные способы исследования задач с параметром: аналитический, графический и комбинированный (функционально - графический). Аналитический – это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра. Графический – это способ, при котором используют графики в координатной плоскости (х; у). Наглядность графического способа помогает найти быстрый путь решения задачи. Из этих двух способов последний является не только изящным, но и наиболее важным, так как в нем просматриваются взаимосвязь между всеми типами математической модели: словесное описание задачи, геометрическая модель – график квадратного трехчлена, аналитическая модель – описание геометрической модели системой неравенств, составленных на основании математических утверждений выявленных по графику квадратичной функции.
Во многих случаях решение квадратных уравнений с параметром приводит к громоздким преобразованиям. Гипотеза: использование свойств квадратичной функции позволит существенно упростить решение, сводя его к решению рациональных неравенств.
Основная часть. Расположение корней квадратного трехчлена на координатной прямой
Рассмотрим некоторые утверждения, связанные с расположением корней квадратного трехчлена f(x)=ax2+bx+с на числовой прямой cотносительно точек m и п таких, что m
x1 и x2 - корни квадратного трехчлена,
D=b2-4ac- дискриминант квадратного трехчлена, D≥0.
m, n, m1, m2, n1, n2 - заданные числа.
Все рассуждения рассматриваются для a>0, случай для a
Утверждение первое
Для того, чтобы число m было расположено между корнями квадратного трехчлена (x1
Доказательство.
при условии x1
Геометрическая интерпретация
Пусть х1 и х2 - корни уравнения. При а > 0 f(x)
Задача 1. При каких значениях k уравнение x2-(2k+1)x + 3k-4=0 имеет два корня, один из которых меньше 2, а другой больше 2?
Решение. f(x)=x2-(2k+1)x + 3k-4; x1
При k>-2 уравнение x2-(2k+1)x + 3k-4=0 имеет два корня, один из которых меньше 2, а другой больше 2.
Ответ: k>-2.
Задача 2. При каких значениях k уравнение kx2+(3k-2)x + k-3=0 имеет корни разных знаков?
Эта задача может быть сформулирована так: при каких значениях k число 0 лежит между корнями данного уравнения.
Решение (1 способ) f(x)= kx2+(3k-2)x + k-3; x1
2 способ решения (использование теоремы Виета). Если квадратное уравнение имеет корни (D>0) и c/a
Задача 3. При каких значениях k уравнение (k2-2)x2+(k2+k-1)x – k3+k2=0 имеет два корня, один из которых меньше k, а другой больше k?
f(x)=(k2-2)x2+(k2+k-1)x – k3+k2; x1 Подставив значения k из найденного множества убедимся в том, что при этих значениях k D>0.
Утверждение второе (а)
Для того, чтобы корни квадратного трехчлена были меньше числа m (x1
Доказательство: x1-m>0, x2-m 0; m2-mx1-mx2+x1x2>0; m2-(x1+x2)m+x1x2
Задача 4. При каких значениях параметра корни уравнения x2-(3k+1)x+2k2+4k-6=0 меньше -1?
D≥0; (3k+1)2-4(2k2+4k-6) ≥0; (k-5)2≥0; k- любое; x0-3/2; k0. 1+(3k+1)+(2k2+4k-6)>0. 2(k+4)(k-1/2)>0. k1/2
Утверждение второе (б)
Для того, чтобы корни квадратного трехчлена были больше числа m (m
D ≥0; x0>m; af(m)>0.
Если выполнено условие m m. Так как m не принадлежит промежутку (x1; x2), то f(m) > О при а > 0 и f(m)
Обратно, пусть выполнена система неравенств. Из условия D > 0 следует существование корней х1 и х2 (х1 m.
Остается показать, что х1 > m. Если D = 0, то х1 = х2 > m. Если же D > 0, то f(х0) = -D/4a и af(x0) О, следовательно, в точках х0 и m функция принимает значения противоположных знаков и х1 принадлежит промежутку (m;х0).
Задача 5. При каких значениях параметра m корни уравнения x2-(3m+1)x+2m2+4m-6=0 a) больше 1? б) меньше -1?
Решение а) D≥0; D≥0; (3m+1)2-4(2m2+4m-6) ≥0; x0>m; x0>1; ½(3m+1)>1; f(m)>0. f(1)>0. 1-(3m+1)+(2m2+4m-6)>0.
(m-5)2≥0; m - любое m>1/3; m>1/3;
(2km-3)(m+2)>0. m3/2. Ответ:m>3/2.
б) D≥0; (3m+1)2-4(2m2+4m-6)≥0; (m-5)2 ≥0; m - любое x0-3/2; m0. 1+(3m+1)+(2m2+4m-6)>0. 2(m+4)(m-1/2)>0. m1/2.
Задача 6. При каких значениях параметра корни уравнения kx2-(2k +1)x+3 k -1=0 больше 1?
Решение. Очевидно, что задача равносильна следующей: при каких значениях параметра m корни квадратного трехчлена больше 1?
D≥0; D≥0 (2k+1)2-4k (3k-1) ≥0; 8k2-8k-1≤0; x0>m; x0>1 (2k+1)/ (2k) >1; 2k+1 > 2k; af(m)>0. af(1)>0. k(k-(2k+1)+(3k-1)) >0. 2k2-2k>0.
Решив эту систему, находим, что
Утверждение третье
Для того, чтобы корни квадратного трехчлена были больше числа m и меньше n (m
D ≥0; m 0 af(n)>0.
Отметим характерные черты графика.
1)Уравнение имеет корни, а значит D > 0.
2) Ось симметрии расположена между прямыми х = m и х = n, а значит m
3) В точках х = m и х = n график расположен выше оси ОХ, следовательно f(m) > 0 и f(n) > 0 (при m
Перечисленные выше условия (1; 2; 3) являются необходимыми и достаточными для искомых значений параметра.
Задача 7. При каких m x2-2mx+m2-2m+5=0 по модулю не превосходят числа 4?
Решение. Условие задачи можно сформулировать следующим образом: при каких m выполняется соотношение -4
Значения т находим из системы
D > 0; m2 - (m2 – 2m + 5) ≥ 0;
4 ≤ х0 ≤ 4; -4 ≤ m≤ 4; f(-4)≥ 0; 16 + 8m+ m2 – 2m + 5 ≥ 0; f(4)≥0; 16-8m + m2-2m + 5 ≥0; решением которой является отрезок . Ответ: m .
Задача 8. При каких значениях m корни квадратного трехчлена
(2m - 2)x2 + (m+1)х + 1 больше -1, но меньше 0 ?
Решение. Значения m можно найти из системы
D≥0; (m+1)2-4(2m-2) ≥ 0;
(2m - 2)/(-1) > 0 (2m -2)(2m -2 -m -1 +1) > 0;
(2m-2)f(0)>0; (2m-2)>0;
Ответ: m > 2.
Утверждение четвертое(а)
Для того, чтобы меньший корень квадратного трехчлена принадлежал интервалу (m;n), а больший не принадлежал (m
D ≥0; af(m)>0 af(n)
График квадратичного трехчлена в точности один раз пересекает ось ОХ на интервале (m; n). Это значит, что в точках х=m и х=n квадратный трехчлен принимает разные по знаку значения.
Задача 10. При каких значениях параметра а только меньший корень квадратного уравнения х2+2ах+а=0 принадлежит интервалу Х(0;3).
Решение. Рассмотрим квадратный трехчлен у(х)= х2-2ах+а. Графиком является парабола. Ветви параболы направлены вверх. Пусть х1 меньший корень квадратного трехчлена. По условию задачи х1 принадлежит промежутку (0;3). Изобразим геометрическую модель задачи, отвечающую условиям задачи.
Перейдем к системе неравенств.
1) Замечаем, что у(0)>0 и у(3) 0. Следовательно, это условие записывать в систему неравенств не нужно.
Итак, получаем следующую систему неравенств:
Ответ: а>1,8.
Утверждение четвертое(б)
Для того, чтобы больший корень квадратного трехчлена принадлежал интервалу (m; n), а меньший не принадлежал (x1
D ≥0; af(m) 0.
Утверждение четвертое (объединенное)
Замечание. Пусть задача сформулирована следующим образом при каких значениях параметра один корень уравнения принадлежит интервалу (ь;т), а другой - не принадлежит? Для решения этой задачи не нужно различать два подслучая, ответ находим из неравенства f(m)·f(n)
D ≥0; f(m)·f(n)
Задача 11. При каких m только один корень уравнения х2-mх+6=0 удовлетворяет условию 2
Решение. На основании утверждения 4(б) значения m найдем из условия f(2)f(5) (10 – 2m)(31 – 5m) m2 - 24 = 0, т. е. при m = ±2√6, При m= -2√6 х = - √6 , который не принадлежит интервалу (2; 5), при m = 2√6 х =√6, принадлежащий интервалу (2; 5).
Ответ: m {2√6} U (5; 31/5).
Утверждение пятое
Для того, чтобы корни квадратного трехчлена удовлетворяли соотношению (x1
D ≥0; af(m)Задача 12. Найти все значения m, при которых неравенство х2+2(m-3)х + m2-6m
Решение. По условию интервал (0; 2) должен содержаться во множестве решений неравенства х2 + 2(m - 3)x + m2 – 6m На основании утверждения 5 значения m находим из системы неравенств f(0) ≤ 0;m2-6m ≤ 0; m f(2) ≤ 0. 4 + 4(m-3) + m2-6m ≤ 0. m [-2;4], откуда m.
Ответ: m .
Утверждение шестое
Для того, чтобы меньший корень квадратного трехчлена принадлежал интервалу (m1; m2), а больший принадлежал интервалу (n1;n2) (m2
D ≥0; af(m1)>0; af(m2)Это утверждение является комбинацией утверждений 4а и 4б. Первые два неравенства гарантируют, что х1(m1, n1), а два последних неравенства – то, что х2(m2, n2),
Задача 13. При какихm один из корней уравнения х2 - (2m + l)x + m2 + m- 2 = 0 находится между числами 1 и 3, а второй - между числами 4 и 6?
Решение. 1 способ. Учитывая, что а = 1, значения m можно найти из системы f(1) > 0; 1 -2m- 1+m2 + т-2 >0; m2-m-2>0 m (-∞;-1) U (2;+∞) f(3)
4(4) 0; 36-12m-6 + m2 + m-2 0 m (-∞;4)U (7;+∞), откуда m(2; 4).
Ответ: m(2; 4).
Таким образом мы установили утверждения, связанные с расположением корней квадратного трехчлена f(x)=ax2+bx+ на числовой прямой cотносительно некоторых точек.
Заключение
В ходе работы я овладела рядом технических и математических умений на уровне свободного их использования и повысила математическую культуру в рамках школьного курса математики.
В результате выполнения работы была выполнена поставленная цель: установлены свойства квадратичной функции, позволяющие существенно упростить решение задач, связанных с расположением корней квадратного уравнения относительно некоторых характерных точек. Установлены возможные случаи расположения корней квадратного трехчлена на числовой прямой. Выявлены алгоритмы, позволяющие решать квадратные уравнения с параметром на основе использования расположения корней квадратного трехчлена на числовой прямой; решены задачи более высокой, по сравнению с обязательным уровнем, сложности. В работе представлено решение только 12 задач в виду ограниченности количества страниц работы. Конечно, рассмотренные в работе задачи можно решить и другими способами: используя формулы корней квадратного уравнения, применяя свойство корней (теорему Виета).
Фактически было решено значительное количество задач. Поэтому было решено создать сборник задач по теме проектно-исследовательской работы «Решебник задач на применение свойств квадратного трехчлена, связанных с расположением его корней на координатной прямой». Кроме того, результатом работы (продуктом проектно-исследовательской работы) является компьютерная презентация, которую можно использовать на занятиях элективного предмета «Решение задач с параметрами».
Презентация к уроку математики в 9 классе по теме "Квадратный трехчлен и его корни" с содержанием заданий углубленного уровня изучения предмета. Презентация расчитана на продолжительное использование в течение всего урока. Задания разного рода по содержанию.
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Пункт плана Пункт плана Пункт плана Пункт плана Пункт плана Актуализация знаний Изучение темы урока Энциклопедическая справка Динамическая минутка Домашнее задание Квадратный трехчлен и его корни подготовила учитель математики: 1КК Радченко Наталья Федоровна
Актуализация знаний Изучение темы урока Энциклопедическая справка Динамическая минута Домашнее задание Актуализация знаний ◊ 1 Повторение материала о функциях; ◊ 2 Теоретические основы решения квадратного уравнения; ◊ 3 Теорема Виета; ◊ 4 Итог.
Актуализация знаний Повторение материала: среди данных функций укажите линейные убывающие функции: y= x²+12 y= -x-24 y= 9x+8 h= 23-23x h= 1/x² g= (x+16)² g= -3
Актуализация знаний Чем определяется наличие и количество корней квадратного уравнения? Как вычислить дискриминант квадратного уравнения D = 2. Назовите формулы корней квадратного уравнения D>0 , то х 1,2 = D = 0 , то х =
Актуализация знаний t² - 2t – 3 = 0 3. Вычислите дискриминант и ответьте на вопрос «Сколько корней имеет квадратное уравнение»? D= 16 >0 , два корня Чему равно произведение корней? Х 1 х 2 = - 3 5. Чему равна сумма корней уравнения? Х 1 + х 2 = 2 6. Что можно сказать о знаках корней? Корни разных знаков 7. Найдите корни подбором. Х 1 = 3, х 2 = -1
Изучение темы урока ◊ 1 Сообщение темы урока; ◊ 2 Теоретические основы понятия «Квадратный трехчлен и его корни»; ◊ 3 Высказывания великих мыслителей о математике; ◊ 4 Разбор примеров тематики; Изучение темы урока Энциклопедическая справка Динамическая минута Домашнее задание
Квадратный трехчлен и его корни Квадратным трехчленом называется многочлен вида ax² + bx + c , где x- переменная, a, b и c - некоторые числа, причем, a≠ 0 . Корнем квадратного трехчлена называется значение переменной, при котором значение этого трехчлена равно нулю Чтобы найти корни квадратного трехчлена ax² + bx + c , необходимо решить квадратное уравнение ax² + bx + c =0
Квадратный трехчлен и его корни Мало иметь хороший ум, главное – хорошо его применять. Р.Декарт Мыслить последовательно, судить доказательно, опровергать неправильные выводы должен уметь всякий: физик и поэт, тракторист и химик. Э. Кольман
Энциклопедическая справка ◊ 1 Понятие «параметр»; ◊ 2 Значение слова «параметр» словарях русского языка и словаре иностранных слов; ◊ 3 Обозначение и широта применения параметра; ◊ 4 Примеры с параметрами. Энциклопедическая справка Динамическая минута Домашнее задание
Энциклопедическая справка ПАРАМЕТР (от греч. παραμετρέω - меряю, c опоставляя). Величина, входящая в математическую формулу и сохраняющая постоянное значение в пределах одного явления или для данной частной задачи…, (мат.) Параметр – постоянная величина, выраженная буквой, сохраняющая свое постоянное значение лишь в условиях данной задачи… «Словарь иностранных слов». 3. При каком значении параметра m квадратный трехчлен 2х ² + 2тх – т – 0,5 имеет единственный корень? Найдите этот корень.
Динамическая пауза ◊ 1 Решение «проблемной задачи»; ◊ 2 Историческая справка: письмо из прошлого; Динамическая минутка Домашнее задание
Динамическая пауза При каком значении параметра т квадратный трехчлен 2х ² + 2тх – т – 0,5 = 0 и меет единственный корень? Найдите этот корень. Квадратное уравнение имеет один корень D=0 D= b² - 4ac; a=2, b=2m, c= - m – 0,5 D= (2m)² - 4 2 (- m – 0,5) = 4m² + 8m +4 D=0, 4m² + 8m +4 = 0 m² + 2m +1 = 0 (m + 1)² = 0 m= - 1 Подставим найденное значение m в исходное уравнение: 2х ² - 2х + 1 – 0,5 = 0 4х ² - 4х + 1 = 0 (2х – 1) ² =0 2х -1 =0 х = 0,5
Динамическая пауза В домашнем задании ученикам 8 класса было предложено найти корни квадратного трехчлена (х ² - 5х +7) ² - 2(х ² - 5х +7) - 3 Подумав, Витя рассудил так: сначала нужно раскрыть скобки, потом привести подобные слагаемые. Но Степа сказал, что есть более простой способ решения и раскрывать скобки вовсе необязательно. Помогите Вите найти рациональный путь решения
Динамическая пауза Задачи на нахождение корней квадратного трехчлена и составление квадратных уравнений встречаются уже в древнеегипетских математических папирусах. Общее правило нахождения корней и решения уравнений вида: ax ² + bx = c, где a > 0, b и c – любые, сформулировал Брахмагупта (VII в. н. э.). Брахмагупта еще не знал, что квадратное уравнение может иметь и отрицательный корень. Бхаскара Ачарья (XII в.) сформулировал, соотношения между коэффициентами уравнения. Составил много задач.
Обобщение, домашнее задание ◊ 1 Решение упражнений с параметром: различные типы заданий; ◊ 2 Итог по изучаемой теме; ◊ 3 Домашнее задание: по уровням. Домашнее задание
Обобщение, домашнее задание Найдите корни квадратного трехчлена (x-4)² +(4y-12)² . Найдите значения параметра a , при каждом из которых квадратный трехчлен x²+ 4 x + 2ax+8a+1 имеет одно решение. Задание на дом: п.3; 1 группа: №45 (в, г), №49(в, г); 2 группа: a) найдите значение параметра а, при котором квадратный трехчлен x²-6x+2ax+4a не имеет решения; b) найдите корни квадратного трехчлена (2x-6)²+(3y-12)²
источник шаблона Чернакова Наталия Владимировна Преподаватель химии и биологии ГОУ НПО Архангельской области «Профессиональное училище №31» «http://pedsovet.su/»
Найти корень квадратного трехчлена можно через дискриминант. Кроме того, для приведенного многочлена второй степени действует теорема Виета, основанная на соотношении коэффициентов.
Инструкция
- Квадратные уравнения – довольно обширная тема в школьной алгебре. Левая часть такого уравнения представляет собой многочлен второй степени вида А х² + B х + C, т.е. выражение из трех одночленов разной степени неизвестной х. Чтобы найти корень квадратного трехчлена, нужно вычислить такое значение х, при котором выполняется равенство этого выражения нулю.
- Для решения квадратного уравнения нужно найти дискриминант. Его формула является следствием выделения полного квадрата многочлена и представляет собой определенное соотношение его коэффициентов:D = B² – 4 А C.
- Дискриминант может принимать различные значения, в том числе быть отрицательным. И если младшие школьники могут с облегчением сказать, что корней у такого уравнения нет, то старшеклассники уже способны их определить, исходя из теории комплексных чисел. Итак, вариантов может быть три: Дискриминант – положительное число. Тогда корни уравнения равны: х1 = (-B + √D)/2 А; х2 = (-B - √D)/2 А;
Дискриминант обратился в ноль. Теоретически в этом случае уравнение также имеет два корня, но практически они одинаковы: х1 = х2 = -B/2 А;
Дискриминант меньше нуля. В расчет вводится некая величина i² = -1, которая позволяет записать комплексное решение: х1 = (-B + i √|D|)/2 А; х2 = (-B - i √|D|)/2 А. - Метод дискриминанта справедлив для любого квадратного уравнения, однако есть ситуации, когда целесообразно применить более быстрый способ, особенно при небольших целочисленных коэффициентах. Этот способ называется теоремой Виета и заключается в паре соотношений между коэффициентами в приведенном трехчлене:х² + P х + Q
х1 + х2 = -P;
х1 х2 = Q.Остается только подобрать корни. - Следует отметить, что уравнение может быть приведено к подобному виду. Для этого нужно разделить все слагаемые трехчлена на коэффициент при старшей степени А:А х² + B х + C |А
х² + B/А х + C/А
х1 + х2 = -B/А;
х1 х2 = C/А.
Учитель высшей категории: Минайченко Н.С., гимназия №24, г.Севастополь
Урок в 8 классе: «Квадратный трёхчлен и его корни»
Тип урока : урок новых знаний.
Цель урока:
организовать деятельность учащихся по закреплению и развитию знаний о разложении квадратного трехчлена на линейные множители, сокращении дробей;
развивать навыки в применении знаний всех способов разложения на множители: вынесение за скобки, с помощью формул сокращенного умножения и способа группировки с целью подготовки к успешной сдаче экзамена по алгебре;
создать условия для развития познавательного интереса к предмету, формирования логического мышления и самоконтроля при использовании разложения на множители.
Оборудование: мультимедийный проектор, экран, презентация: «Корни квадратного трехчлена», кроссворд, тест, раздаточный материал.
Основные понятия . Разложение квадратного трёхчлена на множители.
Самостоятельная деятельность учащихся. Применение теоремы о разложении квадратного трёхчлена на множители при решении задач.
План урока
Решение задач.Ответы на вопросы учащихся
IV. Первичная проверка усвоения знаний. Рефлексия
Сообщение учителя.
Сообщение учащихся
V. Домашнее задание
Запись на доске
Эта тема является основополагающей в разделе «Тождественные преобразования алгебраических выражений». Поэтому важно, чтобы учащиеся автоматически умели не только видеть в примерах формулы разложения на множители, но и применять их в других заданиях: в таких как решение уравнений, преобразование выражений, доказательство тождеств.
В этой теме основное внимание уделяется разложению квадратного трёхчлена на множители:
ax
+ bx + c = a(x – x
)(x – x
 ),
),
где x и x – корни квадратного уравнения ax + bx + c = 0.
– корни квадратного уравнения ax + bx + c = 0.
Это позволяет расширить поле зрения учащегося, научить его мыслить в нестандартной ситуации, используя при этом изучаемый материал, т.е. используя формулу разложения квадратного трёхчлена на множители:
умение сокращать алгебраические дроби;
умение упрощать алгебраические выражения;
умение решать уравнения;
умение доказывать тождества.
Основное содержание урока:
а) 3x + 5x – 2;
б) –x + 16x – 15;
в) x – 12x + 24;
г) –5x + 6x – 1.
№2. Сократите дробь:

№3. Упростите выражение:


№4. Решите уравнение:

б) 
Ход урока:
I. Этап актуализации знаний.
Мотивация учебной деятельности.
а) из истории:
б) кроссворд:
Разминка-тренировка ума – кроссворд:

По горизонтали:
1) Корень второй степени называется…. (квадратный)
2) Значения переменной, при котором уравнение становится верным равенством (корни)
3) Равенство, содержащее неизвестное называется… (уравнение)
4) Индийский ученый , который изложил общее правило решения квадратных уравнений (Брахмагупта)
5) Коэффициенты квадратного уравнения - это… (числа)
6) Древнегреческий ученый, придумавший геометрический метод решения уравнений (Евклид)
7) Теорема, связывающая коэффициенты и корни квадратного уравнения (Виета)
8) «различающий», определяющий корни квадратного уравнения – это… (дискриминант)
Дополнительно:
Если Д>0, сколько корней? (два)
Если Д=0, сколько корней? (один)
Если Д<0, сколько корней? (нет действительных корней)
По горизонтали и вертикали тема урока: «Квадратный трехчлен»
б) мотивация:
Эта тема является основополагающей в разделе «Тождественные преобразования алгебраических выражений». Поэтому важно, чтобы вы автоматически умели не только видеть в примерах формулы разложения на множители, но и применять их в других заданиях: таких как сокращение дробей, решение уравнений, преобразование выражений, доказательство тождеств.
Сегодня мы основное внимание уделим разложению квадратного трёхчлена на множители:
II. Изучение нового материала.
Тема: Квадратный трёхчлен и его корни.
Общая теория многочленов многих переменных далеко выходит за рамки школьного курса. Поэтому мы ограничимся изучением многочленов одной действительной переменной, да и то в простейших случаях. Рассмотрим многочлены одной переменной, приведённые к стандартному виду.


Корнем многочлена называется значение переменной, при котором значение многочлена равно нулю. Значит, чтобы найти корни многочлена, надо приравнять его к нулю, т.е. решить уравнение.
Корень многочлена первой степени  легко найти
легко найти  . Проверка:
. Проверка:  .
.
Корни квадратного трехчлена можно найти, решив уравнение:  .
.
По формуле корней квадратного уравнения находим:
 ;
; 
Если  и
и  -корни квадратного трехчлена
-корни квадратного трехчлена  , где
, где  ≠ 0,
≠ 0,
то .
Доказательство:
Выполним следующие преобразования квадратного трехчлена:
 =
= =
= =
=
= =
= =
=
= =
=
Так как дискриминант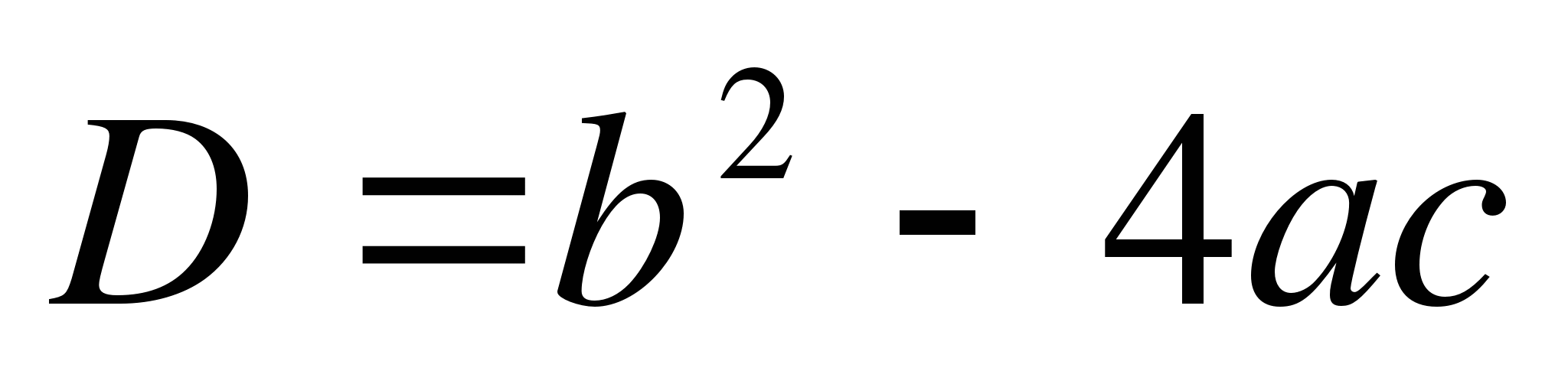 , получим:
, получим:
 =
= =
=
Применим в скобках формулу разности квадратов и получим:
 =
= =
= ,
,
так как  ;
;  . Теорема доказана.
. Теорема доказана.
Полученная формула называется формулой разложения квадратного трехчлена на множители.
III. Формирование умений и навыков.
№1. Разложите на множители квадратный трёхчлен:
а) 3x + 5x – 2;Решение:

Ответ: 3x+5x–2=3(х+2)(х-)=(х+2)(3х-1)
На доске:
б) –5x + 6x – 1;
Дополнительно:
в) x – 12x + 24;
г) –x + 16x – 15.
№2. Сократите дробь:
а)


№4. Решите уравнение:

б) 
IV. Первичная проверка усвоения знаний.
а) Тест.
Вариант 1.
1. Найти корни квадратного трехчлена: 2х 2 -9х-5
Ответ:
2. Какой многочлен надо подставить вместо многоточия, чтобы было верным равенство:
б) Взаимопроверка по вариантам (ответы и параметры оценивания иллюстрируются).
в) Рефлексия.
V. Домашнее задание.